A Burden to America? Immigration and the Economy
The number of immigrants entering the United States legally is greater today than it was at the turn of the century. In fact, after peaking in the early 1900s and registering little activity since, legal immigration has recently surpassed those earlier record levels.1 The current rate of U.S. immigration—the level of immigration adjusted for population—however, is much lower today than it was a century ago. Between 1900 and 1910, about 11 immigrants per thousand residents entered the United States legally. The current rate is about five per thousand, but rising.
Despite the decline in the immigration rate, many Americans still believe that immigration hurts U.S. workers and the economy. Immigrants are perceived as taking jobs away from native-born Americans and filling the rolls for public assistance without paying their share of taxes to replenish the kitty. Nothing could be further from the truth.
A recent report prepared by a panel of economists and sociologists, and published by the National Research Council (NRC), shows that immigrants not only diversify the American economy, but also contribute to economic growth.2 And it is because they are different from natives that the economy as a whole profits. In many instances, immigrants both cause prices to fall, which benefits all consumers, and enable the economy to domestically produce a wider variety of goods than natives alone could.3 If immigrants weren't different from natives, they would only augment the population and the scale of the economy, but not have an effect on the overall growth rate of per capita income.
As the NRC report shows, the overall effect immigration has on gross domestic product is between $1 billion and $10 billion a year. While these amounts may seem negligible in an $8 trillion economy (about one-eighth of 1 percent at most), they are still a gain—and not the drain many believe immigration to be.
How Should Immigration Affect the Economy?
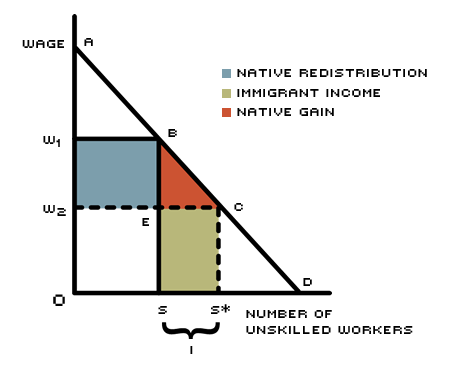
Immigrants increase the supply of labor in the economy. In the most basic labor market scenario, where all workers are producing only one good, this increase—when nothing else changes—will result in a lower market wage for all workers if all workers are the same. But all workers are not the same. Some natives will compete with immigrants for positions because they possess similar skills; others will work alongside immigrants, complementing the immigrants' skills with their own. This skill distinction means that not all native workers will receive a lower wage. Those who compete with—are substitutes for—immigrants will receive a lower wage than they would without immigration, while those who complement immigrants will receive a higher wage.
As explained below, immigration produces net economic gains for all native-born workers, even though one group—which most economists believe to be unskilled domestic workers—experiences a monetary loss (that is, a lower wage). Unskilled domestic workers benefit from the added diversity of goods that immigrants enable the economy to produce. Skilled domestic workers, who are believed to complement immigrant labor, benefit from a higher wage, as well as the added diversity of goods. If the wages of these two groups of native workers did not change in response to immigration, there would be no domestic economic gain for them because the value of the immigrants' production would return directly to the immigrants.
But what if immigrants arrive with skills that do not substitute for any native workers' skills? For instance, what if all immigrants had less than a high school education, while all natives had more than a high school education? Then all native labor would complement immigrant labor and all natives—skilled and unskilled—would gain. On the other hand, what if immigrants were perfect substitutes for native workers, matching the native labor force exactly? That is, what if immigrants arrived in the same proportion of skilled and unskilled workers as the native population? In this case, no loss in native wages would occur. Total national output would increase because immigrants would now produce all of the additional output, and the fruits of their labor would return directly to them. Native workers would be no better or worse off. Thus, natives gain only when the immigrants' skills differ from their own.
To make this account more realistic, assume that the economy now produces two goods instead of just one, as before. Let's call the two goods kibbles and bits. While this change may seem trivial, it opens a new realm of choices for workers and consumers because the relative price—the price of one good in terms of the other—can now change. With this change, workers can now choose which industry they want to work in, with immigration likely influencing the choice.
Producing kibbles requires a lot of unskilled labor and only a little skilled labor. Producing bits requires just the opposite. Without immigration or foreign trade, the economy can efficiently produce and consume a certain amount of kibbles and bits. What happens, then, when unskilled labor immigrates to the economy? As before, the wage of native unskilled workers declines and that of skilled workers increases. And now, because it has become cheaper to produce kibbles, which uses a lot of unskilled labor, their price falls relative to bits. Because of this relative price change, more consumers demand kibbles. Those who really like kibbles gain the most from the price reduction; those who prefer bits don't gain as much. As in the single-good scenario, there are winners and losers.
In addition to lower production costs, the increased supply of unskilled labor also lets some domestic kibbles workers shift to bits production, where they have the comparative advantage over immigrant workers. More kibbles and bits can now be produced because the native labor force is more efficiently allocated as a result of immigration. Thus, in this two-good scenario, the economy gains on two fronts: 1) through a lower relative price for the good that immigrants are better at producing; and 2) through the redistribution of domestic labor to the production of the good for which it has the comparative advantage. Lower prices and greater variety benefit all in the economy.
Legal U.S. Immigrants
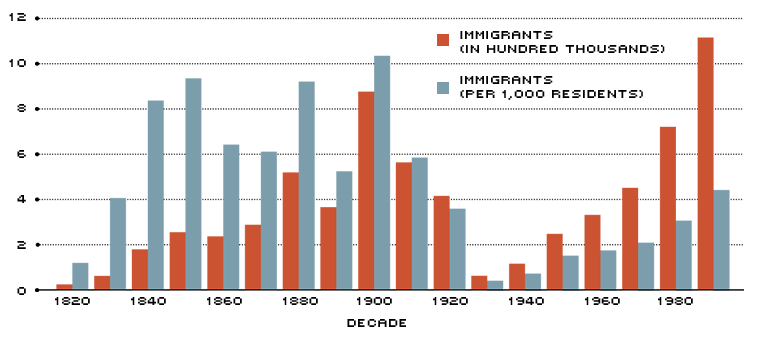
Although recent immigration levels (red bars) have surpassed the records set at the turn of the century, recent immigration rates (blue bars), which adjust for population, are far below rates in the 1800s.
NOTE: Data for the 1980s and 1990s include immigrants who had entered the country illegally, but obtained legal status under the Immigration Reform and Control Act of 1986.
SOURCE: National Research Council (1997), Figures 2.1 and 2.2
How Does Immigration Affect Wages?
The effects of immigration on the U.S. economy have been studied extensively. A common finding of these studies is that immigrants normally receive higher wages in the United States than they would in their native countries. If this weren't true, most would not leave home.4 Still, the majority of recent immigrants earn less than their domestic counterparts. According to the NRC report, the hourly wages of foreign-born men in 1990 were on average 7 percent lower than those of native-born men, and annual earnings were 15 percent lower. This was not true in 1970, though. In that year, the hourly wages of foreign-born men were 1.5 percent greater than those of native- born men, and annual earnings were 3 percent lower.
What could cause such a dramatic shift in 20 years? Two things: 1) the changing mix of countries of origin; and 2) the widening gap in the educational levels of immigrants and their native counterparts. For men, native wages have been quite flat over the past few decades, which implies that the growing wage gap between native- and foreign-born workers stems from an absolute decline in the real wages and earnings of recent immigrants.
In contrast to the men's wage gap, the hourly wages of foreign born women in 1990 were on average only 1.4 percent lower than those of native-born women, with annual earnings 5 percent lower. As with the men, this marks a dramatic shift from 1970, when hourly wages for foreign-born women were 2.5 percent greater than their native counterparts, and annual earnings were 3 percent more. During this 20-year period, the real wages of native-born women have risen, making the widening gap consistent with flat, or moderately rising, immigrant wages. The rapidly increasing employment rates of native women helps explain this growing earnings gap.
A Difference in Skills . . .
Most of the studies on the subject attribute the bulk of the wage gap between immigrants (particularly those from poor countries) and natives to underlying skill differences. In particular, a great deal of evidence suggests that much of the wage gap between Hispanics and non-Hispanics, for example, is due to differences in socioeconomic characteristics, especially educational level and English proficiency. One study found that differences in socioeconomic characteristics accounted for 27 points of a 34 percentage-point wage gap between non-Hispanic white men and men of Mexican ancestry.5 Another study found that, once adjustments had been made for disparities in other socioeconomic characteristics, there was no statistically significant wage difference between non-Hispanic white men and Hispanic men proficient in English.6
The evidence also suggests that the arrival of new immigrants affects the wages of other immigrants more than it does those of natives. For example, a recent study found that a 1 percent increase in the number of recent immigrants causes a nearly 5.6 percent decline in the wages of other recent immigrants.7 The authors also found that, at the same time, wages of earlier immigrants rise, while those of natives decline slightly, leading the authors to conclude that immigration has a rather weak effect on the employment and income of domestic workers.
. . . And in Education
As the composition of immigrant native countries has shifted from Europe to Asia and Central and South America, so has immigrant educational attainment. Despite common perceptions, recent immigrants are generally better educated than earlier ones, even though most recent immigrants are not as well-educated as other U.S. residents. In fact, education levels in the native population have recently accelerated, further widening the gap between natives and immigrants.
| % of immigrants arriving between 1951-60 | % of immigrants arriving in 1993 | % of immigrants with less than a high school education | |
|---|---|---|---|
| Europe | 52.7 | 18.3 | 19.3 |
| Asia | 6.1 | 38.2 | 26.4 |
| Canada | 15.0 | 2.6 | 14.0 |
| Mexico | 11.9 | 14.0 | 76.1 |
| South and Central America | 12.7 | 23.3 | 48.4 |
| Africa | 0.6 | 2.8 | 12.5 |
| Other | 1.0 | 0.7 | 23.8 |
| NOTE: "% of immigrants with less than a high school education" is the percentage of those who immigrated to the United States in 1980-90 who were 25 or older and did not possess a high school degree in 1990. | |||
| SOURCE: Friedberg and Hunt (1995), Table 2, with data from the U.S. Immigration and Naturalization Service and the U.S. Bureau of the Census | |||
As the table above shows, increasing numbers of U.S. immigrants are coming from countries with low levels of average education—generally less than a high school diploma—than before. Despite this shift, a 1995 study still found that immigrants have very little adverse impact on the wages and employment opportunities of natives—even natives with the fewest skills who directly compete with immigrants in the market.8 The authors concluded that there is no evidence that levels of native employment are significantly reduced because of immigration. The authors also noted that most analyses of various countries have found that a 10 percent increase in the immigrant share of the population reduces native wages by 1 percent at most. This finding suggests that most immigrants are not substituting for native labor—skilled or unskilled—but are, instead, complementing it. In fact, over the past two decades, only native high school dropouts—a declining share of the native population—have experienced a decline in their wages because of immigration. No evidence exists that immigration has significantly affected any other group.
Are Immigrants a Fiscal Burden?
Perhaps the most prominent misconception about immigrants is that they are a drain on public coffers. The amount of assistance any group receives, though, depends on its educational level, employment status and inherent wealth. In addition, age at arrival in the country is crucial to determining an immigrant family's impact on a government's budget. For example, an arriving family with young children will require educational services, which are quite costly to the state. At the same time, however, the working immigrant parents pay taxes to help offset the costs of these services.
Older immigrants, who are perhaps already retired, will usually not be able to receive Social Security or Medicare. And currently, they cannot receive Supplemental Security Income (SSI) or, potentially, Medicaid—programs they presumably would not have contributed toward. Young adults without dependents who begin working right away present the smallest burden, and, in fact, will likely become net contributors to government revenues because they will be paying taxes without requiring many services until much further in the future.
Fiscal burdens are also not shared equally across the nation. Immigrants tend to settle in seven states, with California and New York the destination for about half. Not only do these state and local governments have to educate immigrant children, but they also usually have to pay more in income transfers to, and receive less in taxes from, immigrant-headed households, which generally are poorer and have more children than native households. State and local governments, then, rather than the federal government, bear much of the upfront fiscal burden associated with immigrants.
Fiscal relief, however, is not far away. The children of these immigrants will soon enter the labor force and begin paying taxes, thereby supporting not only their kids' education, but also their parents' retirement.9 And, in a matter of two generations, most immigrant families have assimilated to the point that their fiscal burdens are indistinguishable from those of other natives.
The biggest distinction between the first-generation immigrant and native households, though, is not in benefits received, but, rather, in taxes paid. Because they usually earn lower incomes, first-generation immigrant households generally pay less in taxes at every age than natives. Their offspring—second generation immigrants—however, routinely pay more in taxes at every age than natives because they tend to remain in high-income states. When it's all added up, though, most long-run calculations show that immigrants make a net positive contribution to public coffers.
The Tired, The Poor
The huddled masses have been arriving on American shores for more than two centuries now. And, although each new wave of immigrants brings with it a new set of challenges, recent studies show that today's immigrants contribute as much to the economy as yesterday's. Most negative perceptions of immigrants rely on unfounded, and empirically unsupported, assumptions. The evidence, however, shows that immigrants do not take jobs away from, or reduce the wages of, domestic workers—even domestic unskilled workers—but instead expand the economy's capabilities. Although some immigrants may pose an initial fiscal burden to the country, in the long run, the U.S. economy benefits from immigration.
Endnotes
- Illegal immigrants also enter the country, but they are much more difficult to track. According to current estimates, between 200,000 and 300,000 illegal immigrants enter the United States each year, about 40 percent of whom enter legally and overstay their visas. This article focuses on legal immigration. [back to text]
- Much of the information that follows is from the NRC report, which offers an excellent survey of the most current research on immigration. [back to text]
- The bagel is an example of this wider variety of goods. The "skill" to make a bagel came with immigrants earlier this century. [back to text]
- Economic improvement is not the only, or necessarily the most important, reason for people to emigrate to the United States, however. Political considerations and family ties are also strong motives. [back to text]
- See Reimers (1983). [back to text]
- See McManus, Gould and Welch (1983) for the wage results. Zaretsky (1995) explains the concept of statistical significance. [back to text]
- See Greenwood, Hunt and Kohli (1996). [back to text]
- See Friedberg and Hunt (1995). [back to text]
- See Neely (1996) for a description of Social Security's current pay-as-you-go system. [back to text]
References
Friedberg, Rachel M., and Jennifer Hunt. "The Impact of Immigrants on Host Country Wages, Employment and Growth," Journal of Economic Perspectives (Spring 1995), pp. 23-44.
Greenwood, Michael J., Gary Hunt, and Ulrich Kohli. "The Short-Run and Long-Run Factor-Market Consequences of Immigration to the United States." Journal of Regional Science 36:1 (1996), pp. 43-66.
Immigration and Naturalization Service. U.S. Department of Justice. Immigration to the United States in Fiscal Year 1996. www.ins.usdoj.gov/public/stats/971.htm /(May 13, 1997).
McManus, Walter, William Gould, and Finis Welch. "Earnings of Hispanic Men: The Role of English Language Proficiency." Journal of Labor Economics 1:2 (1983), pp. 101-30.
National Research Council Panel on the Demographic and Economic Impacts of Immigration. The New Americans: Economic, Demographic, and Fiscal Effects of Immigration. Report. James P. Smith and Barry Edmonston, eds. Washington, D.C.: National Academy Press, 1997.
Neely, Michelle Clark. "Shaking the Third Rail: Reforming Social Security." The Regional Economist, Federal Reserve Bank of St. Louis (October 1996), pp. 5-9.
Reimers, Cordelia W. "Labor Market Discrimination Against Hispanic and Black Men." Review of Economics and Statistics 65:4 (1983), pp. 570-9.
Zaretsky, Adam M. "How Statistics Can Mislead: The Case of 'Family Caps' in State Welfare Programs." The Regional Economist, Federal Reserve Bank of St. Louis (October 1995), pp. 10-11.
Views expressed in Regional Economist are not necessarily those of the St. Louis Fed or Federal Reserve System.
For the latest insights from our economists and other St. Louis Fed experts, visit On the Economy and subscribe.
Email Us