The Stock Market: Beyond Risk Lies Uncertainty
Life is risky. The future is uncertain. These two phrases, I suppose, we all have heard—and possibly used—many times. Although the words risk and uncertainty seem to cross our lips easily, how well do we understand the concepts? More specifically, are we aware of the implications of risk and uncertainty for stock market investments? If the decline in headline stock market indexes—such as the Dow Jones Industrial Average, the Nasdaq Composite or the S&P 500—over the past two years has reminded you of the possibility of steep declines, stay tuned.
Risk and uncertainty are manifestations of the same underlying force—randomness. In fact, one of the most significant advances in understanding randomness lies in distinguishing between the two concepts. Risk is randomness in which events have measurable probabilities, wrote economist Frank Knight in 1921 in Meaning of Risk and Uncertainty, a seminal treatment on the topic.1 Probabilities may be attained either by deduction—using theoretical models—or induction—using the observed frequency of events. For instance, we can easily deduce the probabilities of the possible outcomes of a game of dice. In a similar vein, economists deduce probability distributions for stock market returns from theoretical models of investor behavior. On the other hand, induction allows us to calculate probabilities from past observations where theoretical models are unavailable, possibly because of a dearth of knowledge about the underlying relation between cause and effect. As an example, we can induce the probability of suffering a head injury when riding a bicycle from observing how frequently it has happened in the past. Similarly, economists estimate probability distributions for stock market returns from the history of past returns.
More intricate than risk is Knight's concept of uncertainty. Whereas risk is quantifiable randomness, uncertainty isn't. It applies to situations in which the world is not well-charted. First, our worldview might be insufficient from the start, like Newtonian mechanics, which was proved to be incomplete by Einstein's relativity. Second, the way the world works itself might change, so that past observations offer little guidance for the future. For instance, once bicyclists were encouraged to wear helmets, the relation between riding the bicycle—the cause—and the probability of suffering a head injury—the effect—changed. You might simply think that the introduction of helmets would have reduced the number of head injuries. Rather, the opposite happened. The number of head injuries actually increased, possibly because helmet-wearing bikers started riding in a more risky manner due to a false perception of safety.2 Paradoxically, the causality between riding the bicycle and suffering a head injury changed because we started managing the observed health risk based on the previously observed relation of cause and effect.
Typically, in situations of choice, risk and uncertainty both apply. Many situations of choice are unprecedented, and uncertainty about the underlying relation between cause and effect abounds.
Given that risk is quantifiable, it is more accessible to theoretical and empirical treatment than is uncertainty. It is thus not surprising that academic literature on stock market randomness deals exclusively with stock market risk. On the other hand, ignorance of uncertainty may be hazardous to the investor's financial health, as the rise and fall of Long-Term Capital Management illustrates. (See more on LTCM's strategy.)
Growth-Optimal Investment
Before turning to an assessment of stock market risk and uncertainty, let us briefly discuss the concept of growth-optimal investing, which is critical to prospering in financial markets. To keep matters simple, we ignore uncertainty. Rather, we go with the quantifiable, that is, risk.
For matters of illustrating risk, let us look at an (admittedly, rather speculative) asset that returns 100 and negative 60 percent per year, respectively, with equal probabilities. The statistical expected return on the asset for the year is simply the average of the two possible returns, 20 percent. Thus, the expected value of a dollar invested in this asset is $1.20 for a one-year investment horizon, $1.44 for a two-year horizon and so on. For maximizing the statistical expected value of final wealth (i.e., wealth at retirement), the investment appears worthwhile. For instance, the expected value of that initial dollar investment 30 years down the line is $237.38.
Oddly enough, the investment in the risky asset is not so worthwhile. The rate of capital growth of the $1 investment (with capital gains and dividends reinvested) approaches negative 10.56 percent per year, which is a far cry from the expected return on capital of 20 percent. On average, the value of the portfolio increases by 100 percent one-half the time and loses 60 percent the other half of the time. Over a two-year period, then, the investor, on average, has only 80 percent of his portfolio value remaining. This amounts to an average rate of capital growth of about negative 10.56 percent per year. So, although the statistical value of the expected final wealth increases with the investment horizon, the probability of the investor actually enjoying this wealth decreases rapidly. Indeed, if the investor is in for the long haul, he almost surely faces financial ruin.3 (Any similarities between the risky asset and tech stocks are coincidental.)
The puzzling difference between the expected return of 20 percent and the expected growth rate of negative 10.56 percent results from the fact that capital growth is multiplicative rather than additive due to compounding. This is why a growth-optimal investment strategy is one that maximizes the statistical expected value of the rate of capital growth, rather than the expected value of final wealth (or, equivalently, expected return). For any investment horizon, a growth-optimal investment strategy almost surely leads to greater final wealth than any other investment strategy. Put differently, the growth-optimal investment strategy almost surely allows the investor to reach any targeted final wealth within the least amount of time. On the other hand, an investor who maximizes expected returns—rather than the expected rate of capital growth—almost surely faces financial ruin in the long haul.
Stock Market Risk
The rate of capital growth of a buy-and-hold portfolio (that is, dividends and capital gains reinvested) in the U.S. stock market is astounding. One dollar invested at the end of 1925 in a buy-and-hold index portfolio of large-capitalization stocks accumulated to $231.22 at the end of 2001, even after adjusting for inflation. The implied average annual rate of growth of this investment equals 7.43 percent. By comparison, the inflation-adjusted average rate of growth of a buy-and-hold investment in long-term corporate bonds averaged only about 2.63 percent. The corresponding numbers for long-term government bonds, intermediate-term government bonds and Treasury bills read 2.18, 2.22 and 0.73 percent.4 The superior performance of stocks relative to other standard types of securities can be seen in other industrialized countries, too, as reported in a study this year by economists Elroy Dimson, Paul Marsh and Mike Staunton.
As for risk, remember that a growth optimal investment strategy almost surely offers an investor higher final wealth than any other investment strategy. Thus, a growth optimal investment strategy already takes due account of risk. In fact, the growth optimal investment strategy is a survival-oriented concept of investment in risky assets. Jeremy Siegel popularized the idea of the stock market as the growth optimal investment strategy in his book Stocks for the Long Run, which was first published in 1994. Not surprisingly, the fraction of families who own (directly or indirectly) publicly traded stocks increased from 40.4 percent to 48.8 percent between 1995 and 1998.5
Stock Market Uncertainty
Stock market uncertainty relates to imperfect information about how the world behaves. First, how well do we understand the process that generated historical stock market returns? More specifically, is the buy-and-hold investment in a stock market index portfolio indeed the growth-optimal investment strategy, as judged by past experience? Second, even if we had perfect information about past processes, can we assume that the same relation between cause and effect will apply in the future? In fact, the aforementioned increase of head injuries in response to our (supposedly) improved understanding of the causality between riding the bicycle and suffering a head injury suggests that this might not be the case.
In trying to answer the question of whether historical data support the hypothesis that a buy-and-hold stock market index portfolio is indeed growth-optimal, it is tempting to look for an answer in stock markets that exist at the present time. But there are pitfalls in this approach. For instance, the aforementioned study by Dimson, Marsh and Staunton analyzes only stock markets that have survived the vagaries of time and, not surprisingly, are found in highly developed, wealthy countries. But there are also those stock markets that have gone under. As economists Robert D. Arnott and Peter L. Bernstein pointed out in a recent article, four stock markets (China, Russia, Argentina and Egypt) suffered total capital loss—that is, a return of negative 100 percent—during the 20th century. Note that every one of these four countries was a significant economic or military power at the time. Focusing on surviving stock markets and, in particular, on the highly successful U.S. stock market distorts the picture—a problem known as survivorship bias.
As for the second question, the one about whether the world will behave in the future as it did in the past, Warren Buffett presented last year an interesting historical example of how our learning about the stock market changes the way the market behaves. Buffett, the world's second-richest man, distinguishes between periods of comparatively high and low stock market valuation. In the early 1920s, stock market valuation was comparatively low, as measured by the inflation-adjusted present value of future dividends. The attractive valuation of stocks relative to bonds became a widely held belief after Edgar Lawrence Smith published in 1924 a book on stock market valuation, titled Common Stocks as Long Term Investments. Smith argued that stocks not only offer dividends, but also capital appreciation through retained earnings. The book, which was reviewed by John Maynard Keynes in 1925, gave cause to an unprecedented stock market appreciation. The inflation-adjusted average annual growth rate of a buy-and-hold investment in large-company stocks established at the end of 1925 amounted to a staggering 32.13 percent at the end of 1928. On the other hand, over the next four years, this portfolio depreciated at an average annual rate of 17.28 percent, inflation-adjusted. Taken together, over the entire seven-year period, the inflation-adjusted average annual growth rate of this portfolio came to a meager 1.11 percent. Buy-and-hold portfolios in the allegedly unattractive long-term corporate and government bonds, on the other hand, grew at inflation-adjusted average annual rates of 10.18 and 9.83 percent, respectively! This proves Buffett's point that, "What the few bought for the right reason in 1925, the many bought for the wrong reason in 1929." We conclude from this episode that learning about the stock market may feed back into the market and, by changing the behavior of the market, render our "learning" useless or, if we don't recognize the feedback effect, hazardous.
Let us now return to the present time. Figure 1 shows that, starting in 1994, the ratio of stock market valuation to (nominal) GNP increased sharply. Although the stock market valuation relative to GNP has declined since its peak in the first quarter of 2000, this ratio is still at an elevated level by historical standards. Is it possible that history is repeating itself? Has learning about stock market risk led to complacency about stock market uncertainty?
The stock market outlook depends on whether the annual rates of growth of a buy-and-hold stock market index portfolio are independent of past rates of growth, or whether nature corrects past above-average growth rates. To help understand this, imagine we flip a coin. We know that, as we keep flipping the coin, the fraction of heads in the total number of tosses converges to one-half. Yet, we also know that each toss is independent of all others. Even if we observe 100 heads in a row, the probability of tails coming up on the next toss is still one-half. The random process dilutes deviations from the mean, rather than correcting them.6 On the other hand, sometimes outcomes are not independent of past realizations. For instance, the expansion of fast-growing companies will slow inevitably because no company can forever grow faster than the economy overall. (Any similarities between mean-reversion of rates of growth and the demise of once-admired tech companies are coincidental.)
Figure 2 exhibits the inflation-adjusted average growth rates of capital invested in a buy-and-hold portfolio of large-company stocks. The black line shows for any given date the average growth rate since year-end 1925. The red line shows for any given date the average growth rate over the prior 10 years. Barring changes in the size distribution of the economy's corporate sector, one might expect the growth rate of capital invested in large-company stocks to be proportional to the long-run growth rate of the economy. Indeed, the average rate of growth for the portfolio established in 1925 seems to approach a constant mean value. The 10-year growth-rate averages, on the other hand, exhibit wild swings around this mean. If the annual growth rates of capital in the stock market are random realizations, the fact that the average rate of capital growth over the past 10 years is above average contains no information for future rates of capital growth. Future realizations will simply dilute the above-average rate of growth of the past 10 years. However, if there is reversion to a constant mean, then the rate of capital growth over the next 10 years of a buy-and-hold portfolio invested in large-company stocks can be expected to be lower than it was in the 1990s. In other words, if there is mean reversion in stock market returns, the odds are stacked against the stock market. Academic evidence on this question is not conclusive though—clearly, a case of uncertainty.
Conclusion
Risk and uncertainty are two concepts that emanate from randomness. Neither concept is fully understood. Although risk is quantifiable, uncertainty is not. Rather, uncertainty arises from imperfect knowledge about the way the world behaves. Most importantly, uncertainty relates to the questions of how to deal with the unprecedented, and whether the world will behave tomorrow the way it behaved in the past.
For investors, not being able to distinguish between risk and uncertainty is hazardous to their financial health. Although we have a fairly good understanding of stock market risk, assessing stock market uncertainty is incomparably harder. Ironically, the lower the level of risk, the more aggressive are investors' bets, and the more vulnerable they are to uncertainty. Clearly, a stock market valuation as elevated as it currently is leaves much room for disappointment.
Ratio of Stock Market Capitalization to Gross National Product
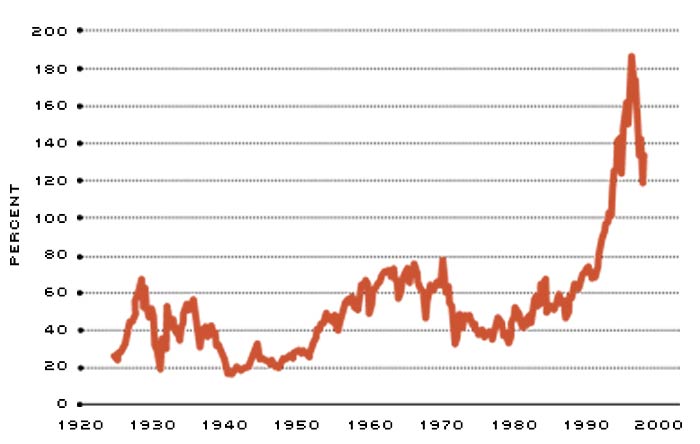
The median of the stock market valuation as a percentage of GNP over the past 76 years is 48.10. The ratio rose dramatically in the last half of the ‘90s. But then it started to fall in the spring of 2000. The observations for this figure were made quarterly, with the first one being made in the fourth quarter of 1925 and the last one in the fourth quarter of 2001.
SOURCES: Haver Analytics for GNP from the first quarter of 1984 through the fourth quarter of 2001, and Balke and Gordon for the GNP prior to the first quarter of 1984. CRSP for total stock market valuation. (CRSP, Center for Research in Security Prices. Graduate School of Business, The University of Chicago, 2002. Used with permission. All rights reserved. www.crsp.uchicago.edu.)
Growth of a Buy-and-Hold Large-Company Stock Index Portfolio
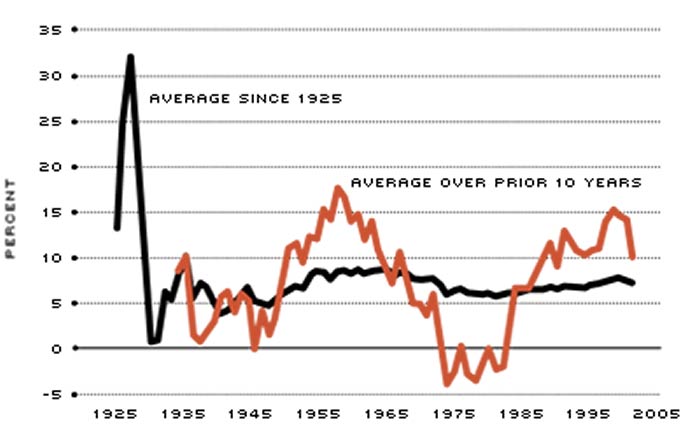
The black line shows for any given date the inflation-adjusted annual average growth rate since year-end 1925. (The first of the annual observations was made in 1926.) The red line shows for any given date the average growth rate over the prior 10 years. If history really does repeat itself, it looks as if the odds are stacked against the stock market for the next several years.
SOURCE: Ibbotson Associates (2002)
Endnotes
- This is the title of what is perhaps the best-known chapter in Knight's book "Risk, Uncertainty, and Profit." [back to text]
- See Barnes (2001) for an article on this topic. [back to text]
- The baffling difference between survival and maximizing the expected value of final wealth is known as the St. Petersburg Paradox. [back to text]
- The data are from Ibbotson Associates (2002). [back to text]
- For a summary of the 1998 Survey of Consumer Finances, see Kennickell, Starr-McCluer and Surette (2000). [back to text]
- Revising up the subjective probability of tails coming up on the next flip after a run of heads is known as the gambler's fallacy. [back to text]
- See Lowenstein (2000, p. 61). [back to text]
- See Shleifer (2000, pp. 107-11). [back to text]
References
Arnott, Robert D. and Bernstein, Peter L. "What Risk Premium is ‘Normal'?" Financial Analysts Journal. March/April 2002, Vol. 58, No. 2, pp. 64-85.
Balke, Nathan S. and Gordon, Robert J. "Appendix B: Historical Data" in: Robert J. Gordon, ed., The American Business Cycle: Continuity and Change. Chicago: University of Chicago Press, 1986, pp. 781-850.
Barnes, Julian E. "A Bicycling Mystery: Head Injuries Piling Up." The New York Times, July 29, 2001, p. 1, col. 3.
Buffett, Warren. "Warren Buffett on the Stock Market," with Carol Loomis, Fortune Investor's Guide 2002, Dec. 10, 2001, pp. 80-94.
Campbell, John Y. and Shiller, Robert J. "Valuation Ratios and the Long-Run Stock Market Outlook: An Update." Working Paper 8221, National Bureau of Economic Research. http://nber.org/papers/w8221.
Dimson, Elroy; Marsh, Paul; and Staunton, Mike. Triumph of the Optimists: 101 Years of Global Investment Returns. Princeton, N.J.: Princeton University Press, 2002.
Ibbotson Associates. Stocks, Bonds, Bills, and Inflation. 2002 Yearbook. Chicago: Ibbotson Associates, 2002.
Kennickell, Arthur B.; Starr-McCluer, Martha; and Surette, Brian J. "Recent Changes in U.S. Family Finances: Results from the 1998 Survey of Consumer Finances." Federal Reserve Bulletin, January 2000, Vol. 86, pp. 1-29, http://www.federalreserve.gov.
Knight, Frank H. Risk, Uncertainty, and Profit. Boston: Houghton Mifflin Co., 1921. Online edition: econlib.org/library/Knight/knRUP.html.
Lowenstein, Roger. When Genius Failed: The Rise and Fall of Long-Term Capital Management. New York: Random House, 2000.
Shleifer, Andrei. Inefficient Markets: An Introduction to Behavioral Finance. Oxford: Oxford University Press, 2000.
Siegel, Jeremy J. Stocks for the Long Run: The Definitive Guide to Financial Market Returns and Long-Term Investment Strategies. 2nd ed., New York: McGraw-Hill, 1998.
Smith, Edgar L. Common Stocks as Long Term Investments. New York: MacMillan, 1924.
Lowenstein, Roger. When Genius Failed: The Rise and Fall of Long-Term Capital Management. New York: Random House, 2000.
Shleifer, Andrei. Inefficient Markets: An Introduction to Behavioral Finance. Oxford: Oxford University Press, 2000.
Views expressed in Regional Economist are not necessarily those of the St. Louis Fed or Federal Reserve System.
For the latest insights from our economists and other St. Louis Fed experts, visit On the Economy and subscribe.
Email Us

