Investment Improvement: Adding Duration to the Toolbox

An increasing number of Americans are taking control of personal investment decisions—whether to meet retirement, children's college education or other financial goals. To do this, they're seeking useful, understandable tools that will guide them in making profitable choices. One tool that investors in fixed-income securities—individual bonds or bond mutual funds—have for assessing risk versus reward is an economic formula known as duration. Although it is far from a perfect measure of risk, duration is a useful supplement to more common, traditionally used measures, like a bond's credit rating and maturity.

Bond Risk Basics

Bond investors face several types of risk. One is credit or default risk; that is, the risk that the bond issuer will not repay the principal invested. Since very few debt issuers default on their obligations, however, it is less of a worry for most investors than another major risk, interest rate risk. This is the risk that the market value of an investment—the price an investor A would receive if an asset were sold today—will change because of changing market interest rates.

The degree of interest rate risk associated with a given fixed-income security (or bond) depends on the size and timing of the cash flows—interest and principal—from that bond. To see this, consider a zero coupon bond, a bond that pays no interest until maturity.1 Because no interest is received until maturity, an investor in a zero coupon bond loses out on any opportunity to reinvest potential earnings at higher market interest rates. In addition, if the investor were forced to sell prior to maturity, he could face a substantial loss if current interest rates on a comparable bond were higher than the interest rate on his zero coupon bond.

However, if the same investor were to purchase a coupon-paying bond—like a U.S. Treasury bond—instead, his interest rate risk in a rising interest rate environment would be reduced since interest or coupon payments received at six-month or year intervals could be reinvested at higher interest rates. This would offset some of the loss that might occur if the investor needed to sell the bond prior to maturity.

Interest rate risk, then, comprises two distinct types of risks, which frequently counteract each other: price or market risk and reinvestment risk. Market risk is the risk that an already-issued bond's market price will fluctuate because of changes in market interest rates. It arises because of the inverse relationship between market interest rates and a bond's price. The longer the maturity of the bond, the greater the market risk since the purchaser of an existing bond with a below-market yield will be stuck with it for as long as he holds the bond. Of course, market risk is not an issue for investors who hold bonds to maturity because the face value, not the market value, of the bond is received at maturity.

Reinvestment risk encompasses the risk that cash flows received from an existing investment, like semiannual coupon payments, could be reinvested at different interest rates than those paid on the existing security. When market interest rates rise, reinvestment risk works in the investor's favor because the cash flows received can be reinvested in higher-yielding securities. When rates fall, however, reinvestment risk works against the investor.

An investor faces market risk and reinvestment risk whenever his planned holding period for a fixed-income security is less than its maturity. These risks tend to work in opposite directions, however: Rising market interest rates increase market risk but decrease reinvestment risk, while declining interest rates decrease market risk but increase reinvestment risk. In other words, an initial capital loss (from rising market interest rates) may, in time, be more than offset by greater returns from reinvested earnings and vice versa.

Duration: The Net Effect

So how does an investor know how much interest rate risk—the net effect of market and reinvestment risk—he's assuming when purchasing a bond or shares in a bond mutual fund? That's where duration comes in. Basically, duration measures the average life of a fixed-income security or a portfolio of securities. It is a more precise measure of the life of a bond than maturity because it takes into consideration any cash flows that are received prior to maturity. In general, the sooner cash flows are received and the larger the amount, the lower the duration, or interest rate risk, of the bond.

More specifically, duration is calculated as the weighted average time to maturity of a bond, using the relative present values of the cash flows from the bond as weights. The calculation yields a single number called Macaulay's duration that is expressed in units of time, which correspond to the receipt of cash flows.2 Macaulay's duration depends on the number of cash flow payment periods and the interval between them, the size of the cash flows and the current yield to maturity of the instrument.3

To see how duration can be used to judge the riskiness of a fixed-income security, consider two bonds, A and B, which on the surface, at least, appear to be very similar. Bond A is a coupon bond with a face value of $1,000 and a maturity of 20 years; its coupon rate is 8 percent, and it pays interest annually. Bond B is a zero coupon U.S. Treasury bond that pays principal and interest of $2,600 at maturity. The current yield to maturity on 20-year bonds is 10 percent. Both bonds yield combined principal and interest of $2,600 over 20 years. Which bond, then, has the most interest rate risk? Although the total cash flows from bonds A and B are equal at maturity, their risk profiles for the intervening years are very different. Bond A has a duration of 9.75 years while Bond B, the zero coupon bond, has a duration of 20 years, equal to its maturity. Bond A has the lower duration and is, therefore, the least risky of the two because the investor will start receiving cash flows much sooner than the holder of Bond B. If an investor were in a position where he would need to sell a bond—all else equal—his capital loss would be lowest with Bond A. The duration of Bond B is twice as large as the duration of Bond A because all of the interest is deferred until maturity.

Duration Dynamics

The example above illustrates how differences in the timing of cash flows change the duration of a bond. Listed below are several other properties of duration that an investor can use either to differentiate the risk characteristics of similar bonds or to anticipate how changes in bond characteristics alter its duration.

• The duration of a bond is always less than its maturity, except for a zero coupon bond, whose duration is always equal to its maturity.
• Duration declines as the coupon rate rises, holding maturity and yield to maturity constant.
• Duration declines as the yield to maturity rises, holding the coupon rate and maturity constant.
• Duration increases as maturity increases, holding the coupon rate and yield to maturity constant.4

Another useful feature of duration is that, by rearranging the duration equation, it can be used to predict the sensitivity of a bond's price to very small increases in interest rates. This rearranged calculation is called modified duration.5 The percentage change in the price of a bond can be approximated by multiplying the percentage point change in the yield to maturity by negative one and the bond's modified duration. The modified duration for Bond A, the 20-year coupon bond with a duration of 9.75 years, is 8.86 years. If market interest rates rise one percentage point to 11 percent, the price of this bond will decline about 8.9 percent to $911.40. For Bond B, the zero coupon bond, a one percentage point increase in market interest rates would lead to a whopping 18.2 percent decline in price. Of course, if interest rates decline one percentage point, Bondholder A would enjoy about a 9 percent capital gain, and Bondholder B would reap an 18 percent gain.

This simple relationship between duration, interest rates and bond prices can help an investor determine an optimal investment strategy based on his expectations about future interest rates.6 For example, if an investor expects interest rates to rise in the near future, he would likely want to keep the duration of his bonds or bond mutual fund short to minimize any potential losses, should a sale become necessary.7 Conversely, in a falling interest rate environment, an investor may want to lengthen the duration of his fixed-income securities, for two reasons; first, he may be able to sell them for a nice gain and second, a longer duration positions an investor to take advantage of a rebound in interest rates, which could lead to profitable reinvestment opportunities. An investor may also wish to use duration to partially hedge or immunize interest rate risk: Market risk and reinvestment risk almost completely offset each other when the duration of a security is equal to the investor's planned holding period.

Duration has been used to measure and hedge interest rate risk to varying degrees by financial institutions and other institutional investors for decades. With an increasing number of brokers and bond mutual fund managers calculating and keeping an eye on duration, individual investors would be wise to add it to their investment toolbox, too.

Thomas A. Pollmann provided research assistance.

Endnotes

1. Zero coupon bonds, like T-bills and certain other instruments, are frequently sold at a discount from their face value and do not pay periodic interest or a coupon. The return, or compounded interest, on these investments is the difference between the discounted purchase price and the face value of the instrument. [back to text]
2. The mathematical formula for Macaulay's duration (D) is:
   
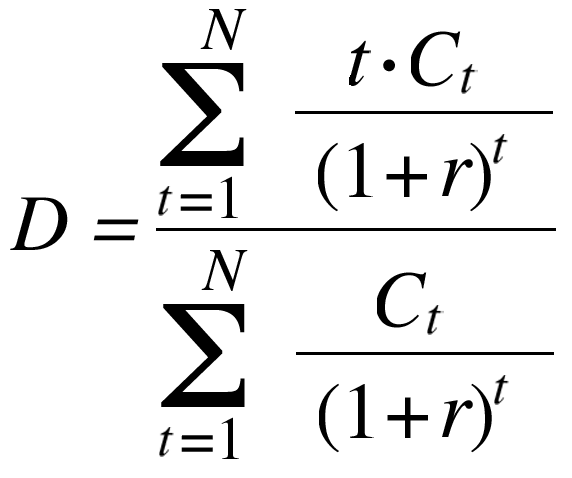
   where N = number of cash flows, t = time to receipt of the cash flow, C_t = cash flow amount in period t, and r = yield to maturity. The expression C_t/(1+r)^t is the present discounted value of the cash flow received in each period t. The sum of all these cash flows is equal to the market value or price of the bond. [back to text]
3. The yield to maturity is the expected rate of return, or interest rate, on a given debt security held until maturity. Because the yield to maturity can be difficult to calculate, the current market interest rate on comparable securities is usually used in the duration calculation. [back to text]
4. This last property only holds true for par and premium bonds. For deep-discount bonds, duration increases with maturity to a distant point and then declines. That's because bonds with really long maturities behave like perpetuities, bonds that pay coupons forever. See Bierwag (1987) or Kritzman (1992) for details. [back to text]
5. The modified duration calculation is: D_m = D/(1 + r) where D_m is modified duration, D is Macaulay's duration and r is the yield to maturity or current market interest rate. [back to text]
6. Duration has its limitations, mostly because it is based on some unrealistic assumptions. For example, duration and modified duration calculations implicitly assume that short-term and long-term interest rates are equal, i.e., the yield curve is flat. See Bierwag (1987). [back to text]
7. The duration of a bond mutual fund is the weighted average of the durations of the individual bonds in the fund. [back to text]

References

Bierwag, Gerald O. Duration Analysis: Managing Interest Rate Risk (Ballinger Publishing Co.,1987).

Kritzman, Mark. "What Practitioners Need to Know About Duration and Convexity," Financial Analysts Journal (November/December 1992), pp. 17-20.

Saunders, Anthony. Financial Institutions Management: A Modern Perspective (Irwin, 1994), Chapter 6.

Williams, Gordon. "Deciphering Duration," Financial World (October 12, 1993), pp. 80-82.