The Return on Investing in a College Education
KEY TAKEAWAYS
- The costs and benefits of a college education—tuition and higher earnings, respectively—can be thought of as if they were the price and payoff of a financial asset.
- Tuition costs have risen sharply and outpaced inflation in recent decades. However, the difference in earnings between workers with and workers without college also grew.
- Estimates of the returns on investing in a college education appear to be significant. In 2020, they ranged from 13.5% to 35.9% across six demographic groups.
To understand the value of higher education, one must compare its costs and benefits. While the costs are immediate, the benefits of education are spread over an entire career. This article calculates college’s costs and benefits and compares them as rates of return.
In drawing this comparison, this article focuses on the economic aspect. It ignores other reasons that one might want a college education, such as better working conditions or the joy of learning, as well as reasons that one might want to avoid college, such as a desire to enter the workforce more quickly.
The Costs and Benefits of Higher Education
The cost of higher education has risen sharply over the last few decades. The first row of the table below shows the average annual tuition for postsecondary institutions offering four-year degrees in 1980, 2000 and 2020. The second row reports the increase in average tuition: For each dollar of tuition paid in 1980, one had to pay $3.70 in 2000 and $8.30 in 2020. The third row of the table reports inflation as measured by the consumer price index: For each dollar of consumption spending in 1980, one had to pay $2.20 in 2000 and $3.30 in 2020. As these factors indicate, the cost of tuition grew more quickly than inflation.
That tuition has risen faster than inflation means that households must have given up more consumption to send their children to college in 2020 than they did in 2000, and even more than they did in 1980. The last row of the table illustrates this point by reporting tuition adjusted for inflation. That is, the last row deflates 2000 and 2020 tuition costs into 1980 dollars.
| 1980 | 2000 | 2020 | ||
|---|---|---|---|---|
| Tuition in 1980, 2000 and 2020 dollars | $3,499 | $12,922 | $29,033 | |
| Cost factor relative to 1980 | 1 | 3.7 | 8.3 | |
| Inflation factor relative to 1980 | 1 | 2.2 | 3.3 | |
| Tuition in 1980 dollars | $3,499 | $5,874 | $8,798 | |
| SOURCES: U.S. Department of Education, Bureau of Labor Statistics and author’s calculations. | ||||
| NOTES: Tuition cost includes total tuition, fees, and room and board from the Digest of Education Statistics, Table 330.10. Inflation is measured using the consumer price index. See the BLS inflation calculator for consumer price index information. | ||||
The pecuniary benefit of higher education is the sequence of earnings one receives throughout a lifetime of work above the earnings that one would have received without higher education. The figure below illustrates a measure of this benefit for white men (I extend the analysis to other demographic groups below): the annual earnings differences, adjusted for inflation, by age between workers with some college education and workers with at most a high school education.
Annual Earnings Difference by Age between Workers with and Workers without College (White Men)
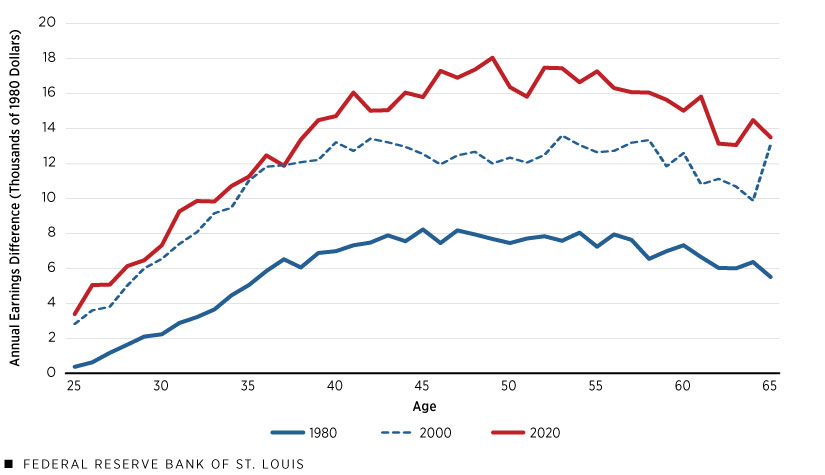
SOURCES: IPUMS USA and author’s calculations.
NOTES: College education means that a worker has attended college but did not necessarily graduate. High school education should be interpreted similarly. Earnings differences are adjusted for inflation.
In 1980, college-educated workers earned more than high school-educated workers, but the difference never exceeded $10,000. In 2000 and 2020, however, the earnings difference was noticeably higher than it was in 1980, even after adjusting for inflation.
What Is the Return on Investing in a College Education?
Suppose one has only a high school education and purchases an asset in 1980 for, say, $13,996 (4 x $3,499—the approximate price of a four-year college education). Suppose, then, that each year for 41 years the asset pays an annual income represented by the blue line for 1980 in the figure above. One would be as well off, economically, as if one had purchased a college education.
Effectively, one’s total income stream—the relatively lower paycheck of a high school-educated worker plus the income from the asset—would mimic that of a college-educated worker. The rate of return on this asset would equal the rate of return on higher education.
Computing the Rate of Return
The concept of present value is key to understanding how to compute the rate of return of an asset. Consider that the price of an apple is the number of dollars one is willing to give up in exchange for the apple. Similarly, the present value of a dollar to be received in the future (say, in one year) is the number of dollars one is willing to give up (invest) today in exchange for the future dollar. Thus, the present value of a future dollar is the price of a future dollar, just like the value of the apple is its price.
The gross rate of return on an asset is the ratio of the present value of future payoffs to the price. (Using the present value in this calculation is a way to adjust for the time that the asset is held, i.e., the present value of a dollar one receives in a year is different from that of a dollar one receives in two years.) Practically, if $1 today is exchanged for $1.10 in a year, then one can infer the present value of that future dollar is $0.91 (because $1/$1.10 = $0.91). Consequently, the gross rate of return is 110% ($1.10/$1 = $1.10), which means that the net rate of return is 10% ($1.10/$1 – $1 = $0.10).
The rate of return on a college education for white men can be computed in the same way as the rate of return on an asset. On average, college-educated workers paid $13,996 (4 x $3,499) in 1980 to receive the extra income represented by the blue line in the figure above throughout the rest of their lives. If one sums up the extra income these workers received and adjusts for the time it took to get this income, the rate of return on the college tuition they paid is very large at 20.5%.
The table below shows the rates of return on a college education for six demographic groups in 1980, 2000 and 2020. Although the rates of return vary greatly across time, gender and race, they are high relative to the returns one finds in financial markets. In all three years, the highest rates of return are for Asian men and Asian women. Black men and Black women have the lowest rates of return in two of the three years.
| White Men | White Women | Black Men | Black Women | Asian Men | Asian Women | |
|---|---|---|---|---|---|---|
| 1980 | 20.5% | 21.6% | 22.9% | 23.9% | 24.6% | 26.1% |
| 2000 | 29.1% | 25.6% | 22.1% | 21.0% | 56.3% | 36.7% |
| 2020 | 24.1% | 22.7% | 14.2% | 13.5% | 35.9% | 31.1% |
| SOURCES: IPUMS USA and author’s calculations. | ||||||
| NOTE: Asian comprises Chinese, Japanese and other Asian or Pacific Islander. | ||||||
What Is Missing?
The calculation described above is intuitive, but it abstracts considerations that may affect the estimated rates of return on a college education. These considerations include a selection issue, an employment issue, a mortality issue and a nonpecuniary benefits issue.
The “Selection” Issue
I computed rates of return using earnings from college-educated workers. It is possible, however, that college-educated workers have skills—acquired before they even attended college—that make them simultaneously better at earning high incomes and more likely to pursue a degree. This consideration means that the calculation tends to overstate the return on education because it conflates the actual return with the likely higher skill level of college-educated workers.
The Employment Issue
Earnings are available only for employed workers. So, the calculation implicitly assumes that all workers have the same (zero) rate of unemployment. In fact, however, high school-educated workers typically experience higher rates of unemployment. The implicit assumption that all workers are continuously employed is likely to mean that the calculation underestimates the return on education.
The Mortality Issue
Unlike a financial asset that may be passed on to one’s children, one must remain alive to reap the benefit of education. Individuals know this when they decide whether to pursue higher education and how much they are willing to pay for it. Yet, the calculation assumes that all individuals live to 65, regardless of year, race and gender. Therefore, the calculation overestimates the return on education for workers who are the most likely to die before they reach 65.
The Nonpecuniary Benefits Issue
The calculation does not address the nonpecuniary benefits of an education. For example, high school-educated and college-educated workers may work different hours or in different conditions. In the same vein, the calculation is silent about the enjoyment, or lack thereof, that one might obtain from working.
The Return on Investing in College Appears to Be High
Education has a return in essentially the same way any asset does: There is an initial investment entitling the investor to a subsequent stream of income. Comparing higher education’s cost (in this case tuition, which is the initial investment) and its benefit (the higher incomes that college-educated workers earn) as if they were the price and payoff of a financial asset yields estimates of a return that appears to be quite high. This should not be a surprise: Despite rising tuition over the years, college enrollment rates are still high because students and their families recognize that the payoff can be greater.
Views expressed in Regional Economist are not necessarily those of the St. Louis Fed or Federal Reserve System.
For the latest insights from our economists and other St. Louis Fed experts, visit On the Economy and subscribe.
Email Us


