How Does Compound Interest Work?
Legend has it that Albert Einstein once declared compound interest as the eighth wonder of the world. True or not, this quote has been repeated over and over, demonstrating its merit.
What is compound interest? This powerful force allows someone to invest a sum of money today that will grow into a much larger amount.
For savers, it means earning interest on your original principal—plus on the interest your investment generates. Compound interest is sometimes described as “interest on interest” because earned interest essentially gets added to the principal over time. Savings vehicles such as certificates of deposit typically pay compound interest.
For borrowers, it means that owed interest is being calculated on your unpaid balance, plus on previous interest charges left unpaid. This is how credit card debt can balloon if left unchecked.
I’d argue that taking advantage of compound interest is the single most powerful action that an individual investor can leverage to build wealth.
Let’s run through a few examples to better understand the power of compound interest for savers.
How the Rule of 72 Works
The Rule of 72 is an easy compound interest calculation to quickly determine how long it will take to double your money based on the interest rate. Simply divide 72 by the interest rate to determine the outcome. At a 2% interest rate, it would take 36 years to double your money. At a 12% interest rate, it would only take six years to double your money.
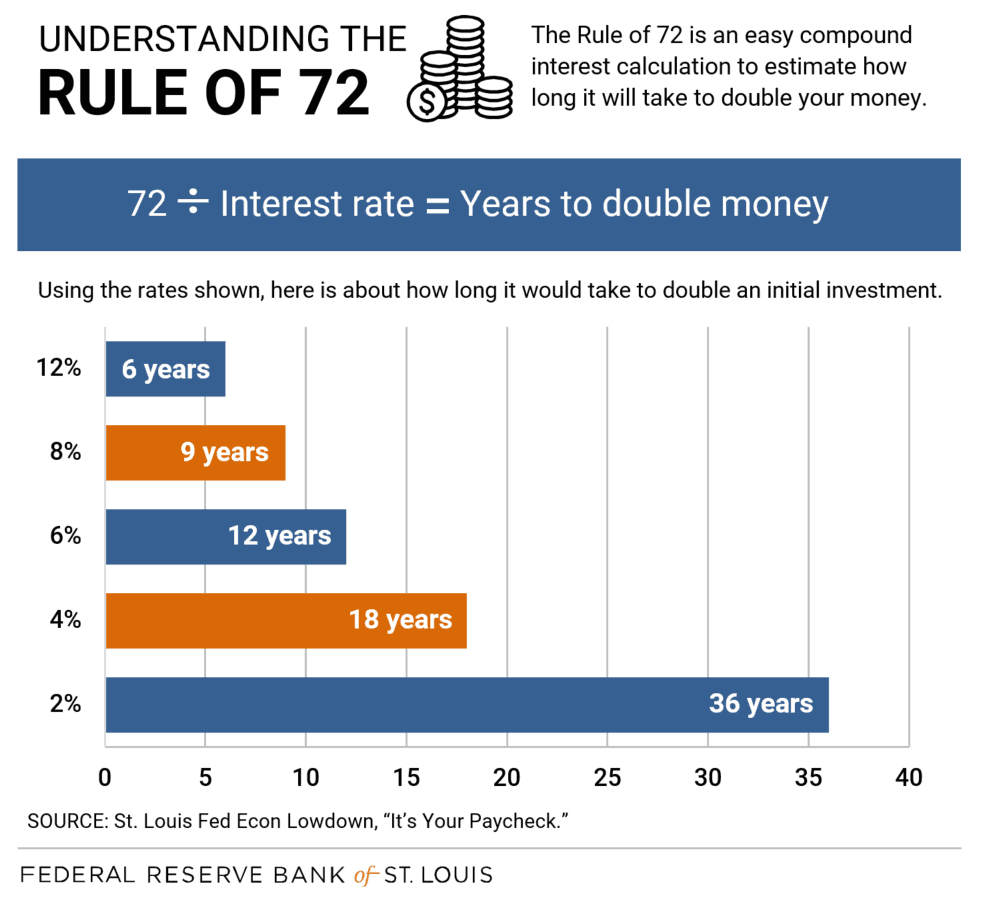
You can also use the Rule of 72 to approximate how much an amount would grow over a time period. Let’s say you wanted to set aside $5,000. How would your investment grow after 36 years with a 2% versus 8% interest rate? (We’ll assume you don’t make any additional contributions to the principal and that interest is compounded annually.)
How long will it take to double your money at 2% interest?
- Using the Rule of 72: We know that 72÷2=36, so $5,000 would double to $10,000 during our 36-year time frame.
- Using Investor.gov compound interest calculator: The result is pretty close. The calculator shows $5,000 would be worth about $10,200 after 36 years.
How long will it take to double your money at 8% interest?
- Using the Rule of 72: Time for math. If we divide 72÷8, the answer is nine. That means your $5,000 would double in about nine years. But wait—you have 36 years. Your money will double four times in that period (36÷9=4)! The first nine years, it doubles to $10,000. After 18 years, that amount doubles to $20,000. After 27, that amount doubles to $40,000. And finally, $40,000 doubles to $80,000 at 36 years.
- Using Investor.gov compound interest calculator: Close again; $5,000 would be worth about $79,840 after 36 years.
Test your knowledge
Got the hang of the Rule of 72? Try estimating how $5,000 would grow at 12% over 36 years. Tap "answer" below when ready to check your comprehension.
Using the Rule of 72: 72÷12=6. Your money will double every six years. Because 36÷6=6, it will double six times. So, $5,000 becomes $10,000, then $20,000, then $40,000, then $80,000, then $160,000, and finally $320,000.
Using Investor.gov compound interest calculator: Assuming you don’t make any additional contributions to the principal, and that interest compounds annually, the calculator shows $5,000 would be worth about $295,680 after 36 years. The Rule of 72 is intended as an approximation.
These examples illustrate the importance of the interest rate and duration of your investments. With that being said, risk tolerance should always be considered with higher interest rates; a higher rate of return generally comes with additional risk.
The Importance of Investing Early to Earn Interest
There’s a saying: “The best time to plant a tree was 20 years ago. The second best time is now.” The same can be said for taking advantage of compound interest. This illustration shows how the earlier someone can start investing, the more time money will have to grow.
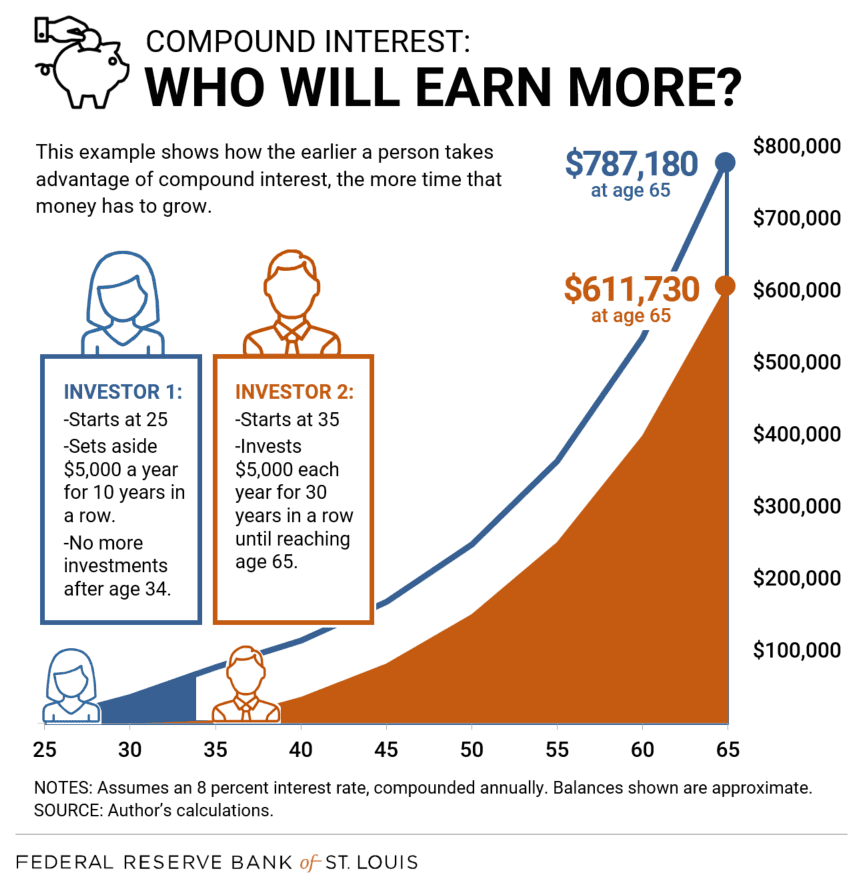
For an example of compound interest, let’s assume an 8% interest rate with a retirement age of 65. Interest is compounded annually.
- A 25-year-old invests $5,000 every year for 10 consecutive years. After age 34, no additional investments are made and the money is left to grow until the investor reaches age 65.
- A 35-year-old invests $5,000 every year for 30 consecutive years until retiring at age 65.
Who do you think will have more money at 65?
- The individual who started investing at 25 years old and made 10 total payments of $5,000 will end up with approximately $787,180 at age 65.
- The 35-year-old who made 30 total payments of $5,000 will end up with approximately $611,730 at age 65.
Remember: Inflation Affects Future Purchasing Power
We’d be remiss to talk about future projections without mentioning inflation. Inflation occurs when the prices of goods and services increase over time. The Federal Reserve's "dual mandate" includes keeping prices stable, and monetary policymakers have equated price stability with a low, measured inflation rate targeted at 2% over the longer run.
The point is to illustrate that the purchasing power of money is expected to be less in the future. This should always be considered when reviewing long-term projections. For instance, the purchasing power of $787,180 today would be approximately $434,580 in 30 years, assuming a 2% average inflation rate.
Summary
The power of compound interest can be difficult to grasp. This post provided a few situations to illustrate the impact compound interest can have over time. The Rule of 72 shows how quickly money can double depending on the interest rate. For those interested in saving money, compound interest is a powerful thing to understand—perhaps even the “eighth wonder of the world.”
Additional Resources
- YouTube Video: Growing Money–Compound Interest
- YouTube Video: Inflation and Interest Rates
This blog explains everyday economics and the Fed, while also spotlighting St. Louis Fed people and programs. Views expressed are not necessarily those of the St. Louis Fed or Federal Reserve System.
Email Us


