How Quickly Can Monthly Inflation Predict Annual Inflation?
After peaking at 7.1% in June 2022, inflation—measured as the year-over-year percent change in the personal consumption expenditures (PCE) price index—has been falling toward the Federal Reserve’s target of 2%. As of April 2024, PCE inflation (the Fed’s preferred measure) stood at 2.7%.
Because inflation is typically measured over the past year, it is inherently a slow-moving and backward-looking measure. Even if monthly inflation were to fall to zero, it would take a few months before annual inflation hit 2%.
As inflation gradually eases, how soon will economists know when annual inflation returns to 2%? In today’s blog post, I examine how quickly one might be able to confidently predict this using monthly inflation data.
Higher-Frequency Data Are Noisy
Looking at higher-frequency data—e.g. the percent change over the last month or quarter—may be valuable for getting a more accurate real-time estimate of inflation. However, monthly and quarterly measures of inflation bring their own problems because they both fluctuate quite dramatically. In the figure below, I show PCE inflation measured at the annual, quarterly and monthly levels. Quarterly inflation is the percent change in prices over the last three months, while monthly inflation is the percent change over the last month. To make these measures comparable, I annualized the quarterly and monthly measures by multiplying them by 4 and 12, respectively.
The Volatility of Inflation Rates
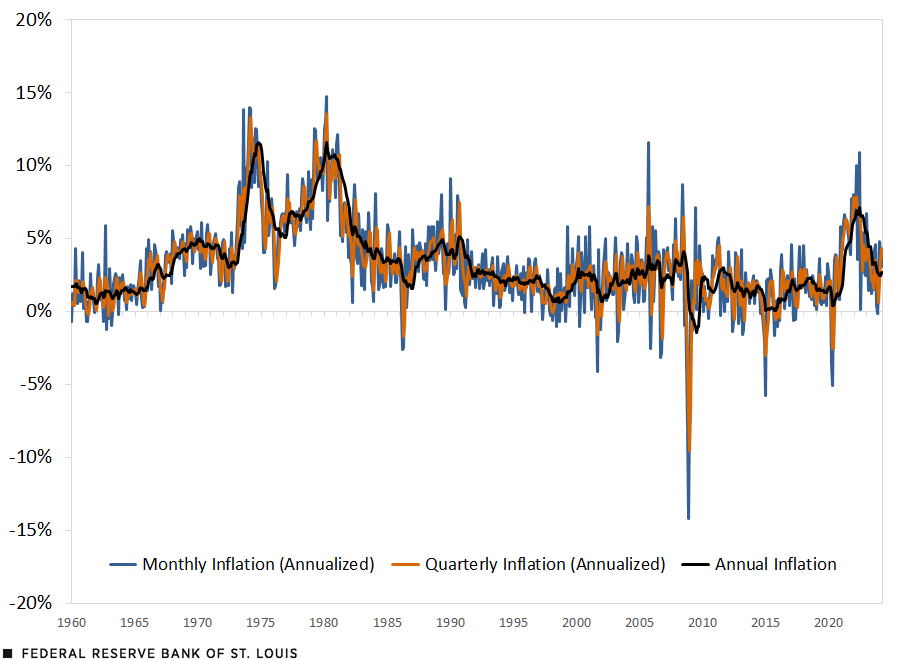
SOURCES: Bureau of Labor Statistics and author’s calculations.
NOTE: The data begin in January 1960 and end in April 2024.
The figure shows that quarterly and monthly measures are substantially more volatile than the annual measure. This could be driven by short-term fluctuations, which may or may not persist, or by statistical noise. In general, economists prefer to focus on annual inflation because it is less noisy, and less likely to be driven by transitory shocks.
Predicting Annual Inflation with Monthly Data
How well can we predict inflation over a full year if we have only the first few months of data? To operationalize this, I ran a regression analysis, using a few months of data to predict the full year of inflation. In particular, I modeled inflation using the following linear regression:
α + β * Annualized Inflation over Next X Months + γ * Inflation over Last 12 Months + εThis linear regression is as follows: Inflation over the next 12 months is equal to alpha plus beta times annualized inflation over next x months plus gamma times inflation over the last 12 months plus epsilon.
where ε is the error term, and X is a number from 1 to 12. I annualized inflation over the next X months in the same way as before (I divide by the number of months and multiply by 12).The variable of inflation over the last 12 months is the inflation over the 12-month period before the start of the new monthly data. I ran this regression separately for each horizon X, starting in January 1990 and continuing to the most recent available data.I use only data going back to January 1990 because inflation seems to have entered a new regime of low, stable inflation after the 1980s. If I were to have included earlier years, it would appear that monthly inflation had higher predictive power, since it is indicative of the inflation regime the economy is in. The results of the regression analysis are in the table below.
| Horizon (X Months) | α | β | γ | R2 |
|---|---|---|---|---|
| 1 | 1.2% | 0.22 | 0.22 | 28% |
| 2 | 1.1% | 0.33 | 0.18 | 38% |
| 3 | 0.9% | 0.43 | 0.15 | 48% |
| 4 | 0.8% | 0.53 | 0.12 | 56% |
| 5 | 0.7% | 0.61 | 0.09 | 64% |
| 6 | 0.5% | 0.69 | 0.06 | 71% |
| 7 | 0.4% | 0.76 | 0.04 | 78% |
| 8 | 0.3% | 0.83 | 0.02 | 84% |
| 9 | 0.2% | 0.88 | 0.01 | 89% |
| 10 | 0.2% | 0.93 | 0.00 | 94% |
| 11 | 0.1% | 0.97 | 0.00 | 98% |
| 12 | 0.0% | 1.00 | 0.00 | 100% |
| SOURCE: Author’s calculations. | ||||
To see how the predictive power of the regression changes as we get more months of data, we first focus on the R2, which indicates the share of the variance of the outcome that is explained by the predictors (i.e., inflation over the next X months and inflation over the last 12 months). The R2 begins at 28% when we have only one month of data, rises to 71% with six months of data, and mechanically reaches 100% once we have all 12 months. (This is mechanical because once we have all 12 months of data, we know exactly what inflation has been over those 12 months.) However, the relationship is not just mechanical because it also reflects the fact that inflation is correlated over time: Inflation over the first six months of the year is useful for predicting what inflation will be over the next six months. Once we reach seven months of data, we can already explain over three-quarters of the variance of inflation.
We can also look at the coefficients from this regression at different horizons. With only a few months of data, the coefficient of the current year’s inflation data (β) and the coefficient of the prior year’s inflation data (γ) are both modest but important. When there are relatively little data for the current year, the prior year’s inflation is informative, as noted by the value of γ in the table above. However, as more data come in for the year, the coefficient on the prior year’s inflation goes to zero, while the coefficient on the current year’s data goes to 1.
How Soon Would We Know When Annual Inflation Reaches 2%?
Imagine that PCE inflation started to come in at 2% each month, starting in May 2024. We can use the results of these regressions to simulate how quickly we could tell that inflation had fallen to an annual inflation rate of 2%. The regression coefficients tell us the predicted value of annual inflation in April 2025 and allow us to see how this prediction would change as successive months of 2% inflation materialized. If we assume that the residuals are normally distributed (this is a reasonably accurate approximation of the data), then we can use the standard deviation of the error term to get the 95% confidence interval (CI) for inflation.Inflation will be within the 95% confidence interval 95% of the time. The formula for the 95% confidence interval is Predicted Value +-1.96 * Standard Deviation of Error Term.The predicted value plus negative 1.96 times the standard deviation of the error term.
| Horizon (X Months) |
Predicted Annual Inflation in April 2025 after X Months of 2% Inflation |
Lower Bound of 95% CI | Upper Bound of 95% CI |
|---|---|---|---|
| 1 | 2.22% | 0.06% | 4.38% |
| 2 | 2.19% | 0.17% | 4.20% |
| 3 | 2.16% | 0.29% | 4.02% |
| 4 | 2.13% | 0.42% | 3.84% |
| 5 | 2.10% | 0.55% | 3.66% |
| 6 | 2.08% | 0.68% | 3.47% |
| 7 | 2.06% | 0.83% | 3.29% |
| 8 | 2.04% | 0.99% | 3.09% |
| 9 | 2.02% | 1.17% | 2.88% |
| 10 | 2.01% | 1.37% | 2.66% |
| 11 | 2.00% | 1.62% | 2.38% |
| 12 | 2.00% | 2.00% | 2.00% |
The results, shown in the table above, suggest that if monthly inflation suddenly dropped to 2%, we would start to know within a few months. After six months of 2% inflation, we would have a predicted value of 2.08% for April 2025 inflation, with a 95% confidence interval ranging from 0.68% to 3.47%. It would take a full nine months of data before we could say, with 95% confidence, that annual inflation would come in below 3%. Although this model cannot predict exactly when 2% annual inflation is reached, one may not have to wait a whole year to find out.
Notes
- The variable of inflation over the last 12 months is the inflation over the 12-month period before the start of the new monthly data.
- I use only data going back to January 1990 because inflation seems to have entered a new regime of low, stable inflation after the 1980s. If I were to have included earlier years, it would appear that monthly inflation had higher predictive power, since it is indicative of the inflation regime the economy is in.
- Inflation will be within the 95% confidence interval 95% of the time. The formula for the 95% confidence interval is Predicted Value +-1.96 * Standard Deviation of Error Term.The predicted value plus negative 1.96 times the standard deviation of the error term.
Citation
Jeremy Majerovitz, ldquoHow Quickly Can Monthly Inflation Predict Annual Inflation?,rdquo St. Louis Fed On the Economy, June 25, 2024.
This blog offers commentary, analysis and data from our economists and experts. Views expressed are not necessarily those of the St. Louis Fed or Federal Reserve System.
Email Us
All other blog-related questions


