Is the U.S. Economic Expansion Due to End?

In her Dec. 16, 2015, press conference, then-Federal Reserve Chair Janet Yellen famously stated “I think it’s a myth that expansions die of old age. I do not think that they die of old age. So the fact that this has been quite a long expansion doesn’t lead me to believe that…its days are numbered.” See Board of Governors of the Federal Reserve System. “Transcript of Chair Yellen’s Press Conference.” Dec. 16, 2015.

Nevertheless, there remains an idea in the public forum that the longer the expansion, the more likely that it will end. In the field of statistics, this is known as positive duration dependence.

Think of it this way. We are currently in an expansion, and the almighty flips a weighted coin:

• If it turns up heads, we remain in the expansion next year.
• Otherwise, we will be in a recession next year.

Positive duration dependence is present if, as the expansion continues, the coin is increasingly weighted so that it turns up tails.

And yet we know expansions always end in the U.S.Australia, though, is in year 28 of an expansion. So maybe it’s not true Down Under? Isn’t this type of dependence obvious? Not quite. Even if the dependence was negative—meaning the coin is decreasingly likely to turn up tails as the expansion continues—a recession will occur eventually. The fact that expansions end is insufficient to identify duration dependence of any kind.

It’s just for this reason that biostatisticians have developed survivor analysis (though they had in mind the lifespans of people rather than stages of the business cycle).

One method frequently used in survival analysis is the hazard function, which plots the rate of failure for a system or part over a future period conditional on the age of that system or part. For example, in the case of human lifespans, the hazard function would plot the probability of dying in the next year conditional on how old a person is.

We applied this method to the business cycle, estimating the probability that an expansion will die (that is, a recession will occur) in the next month conditional on the age of the expansion (that is, the number of months since the previous recession). In the figure below, we report estimated hazard functions associated with U.S. expansions that began both before and after World War II.We estimate these probabilities by assuming a Weibull distribution as in Rudebusch, Glenn D. “Will the Economic Recovery Die of Old Age?” Federal Reserve Bank of San Francisco Economic Letter 2016-03, Feb. 4, 2016.

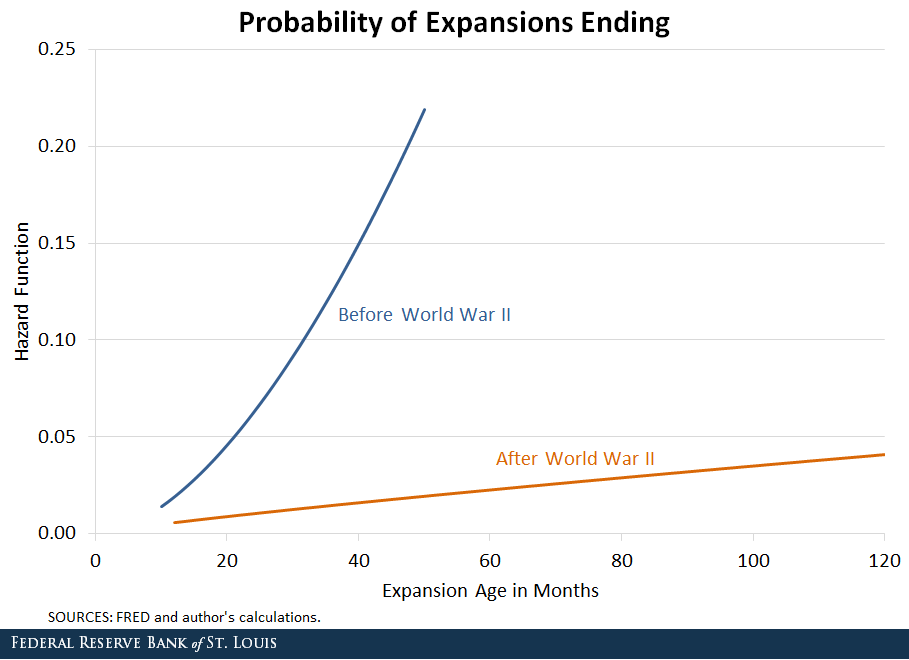
One can interpret the lines as being the probabilities of the coin landing on tails in our example from above. As we move from left to right, we see that the estimated probabilities were increasing in age for both the prewar and postwar periods. This means that a recession was more likely to occur the older it was.

However, there is a stark difference in the slopes of the two lines. In the prewar period, the probability of a recession occurring in the next month rose sharply as the age of the expansion increased. It rose from around 5 percent when the expansion was 2 years old to over 20 percent when the expansion was 4 years old.

On the other hand, the hazard function in the postwar period was much flatter. The recession probability increased from about 1 percent at 2 years old to just over 4 percent at 10 years old. These results suggest that the age of an expansion has been much less of a factor in bringing about its end since World War II.

While one could interpret the figure as indicative of positive duration dependence, it is clearly insufficient for forecasting the end of an expansion. Other factors play a role as well.

Consider an analogy with two adults:

• The first is a 25-year-old chain-smoker and heavy drinker who juggles chainsaws for a living.
• The second is a 70-year-old in perfect health.

Who is more likely to die next year? Using data on the U.S. population, an estimated hazard function based purely on age would obviously predict a much higher likelihood of dying for the 70-year-old. And yet, my money is on the 25-year-old. Clearly, age is not the only relevant factor when predicting a person’s death.

Similarly, there are many other factors that economists consider when forecasting when the next recession will occur. Popular predictors include residential investment, the slope of the yield curve and employment growth.

Now that expansions don’t seem to be dying of old age anymore, gauging the health of the economy through these other measures is much more useful than simply expecting a recession to occur because we’re due for one.

¹ See Board of Governors of the Federal Reserve System. “Transcript of Chair Yellen’s Press Conference.” Dec. 16, 2015.

² Australia, though, is in year 28 of an expansion. So maybe it’s not true Down Under?

³ We estimate these probabilities by assuming a Weibull distribution as in Rudebusch, Glenn D. “Will the Economic Recovery Die of Old Age?” Federal Reserve Bank of San Francisco Economic Letter 2016-03, Feb. 4, 2016.

• On the Economy: Housing Indicators to Watch in 2019
• On the Economy: U.S. Economy Contracting in Q1? Happens Almost Every Year
• On the Economy: Can an Inverted Yield Curve Cause a Recession?