Liftoff and the Natural Rate of Interest

Thinkstock/Willard

Financial markets have become focused on if and when the Federal Reserve should “lift off,” that is, depart from its zero interest rate policy. In a recent Economic Synopses essay, I discussed issues related to liftoff. This post draws from that article to discuss liftoff using two concepts from a central banker’s toolkit: the natural rate of interest and monetary policy.

Central bankers often talk about monetary policy with respect to the natural real interest rate, also called the natural rate or the equilibrium real interest rate. This natural rate has been described as “the real interest rate consistent with output equaling the natural rate of output and stable inflation.”¹ Thus, the Fed can achieve its dual mandate if it can get the actual real interest rate to equal the natural rate. Because there are costs associated with rapid interest rate changes, a central bank may prefer to move the actual rate toward the natural rate gradually.

Importantly, the natural rate cannot be directly measured, unlike nominal interest rates or stock prices. Despite the measurement problem, the natural rate is viewed, in some circles, as a useful concept for the Federal Open Market Committee (FOMC) in setting the federal funds rate.

So the $64,000 question is: What is value of the natural rate today?

The Taylor Rule

John Taylor of Stanford University, the economist who first applied the natural rate to a specific, practical monetary policy rule, sets its value at 2 percent.² His formula is known as the Taylor rule. The natural rate is one component of that formula.

Taylor also makes the case that, in periods of successful monetary policy, the federal funds rate has closely tracked the rate implied by the Taylor rule. In his view, the Taylor rule is descriptive of these successful episodes (from a macroeconomic perspective) in the past and also prescriptive for the future. The figure below plots the real interest rate implied by the Taylor rule between 1995 and 2014 (the orange line, using 2 percent as the natural rate) and the historical real federal funds rate (the blue line).³

The nominal federal funds rate is bounded below by zero, but this zero bound doesn’t imply a lower bound on the (expected) real interest rate. However, if inflation expectations are well-anchored at least in the short run, then the short-term real rate could be considered to also have a lower bound.⁴

I plotted a “real rate lower bound” as the black horizontal line at -2 percent: Since I plotted the Taylor-rule-implied rate and historical federal funds rate in real terms, I plotted the lower bound on the interest rate in real terms as well. I chose -2 percent, or zero minus the FOMC’s stated inflation target of 2 percent.

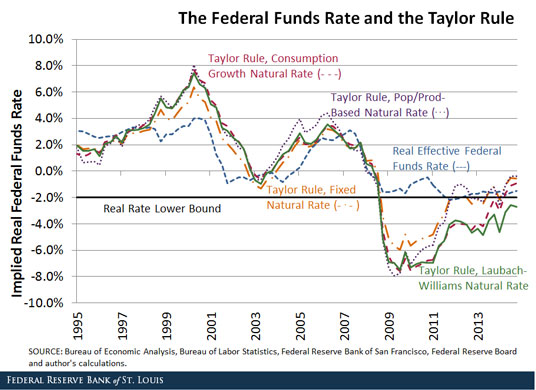
Three things jump out when examining the post-2007 side of the figure. First, the Taylor rule rate fell dramatically below the lower bound during the financial crisis, primarily because of a large deviation of output from its potential. When output declined during the recession and stayed below its long-run historical trend, the Taylor rule implied that the real rate should fall substantially below zero.

Second, the actual federal funds rate did not track the Taylor-rule rate at this time because of the lower bound on interest rates. While the Taylor rule called for dramatic policy accommodation, this eventually became infeasible because of the lower bound.

Third, over the past year or so, the Taylor rule rate has been above the lower bound since the gap between actual and potential output largely closed as the economy began to recover. In practical terms, it means that if one were to use the Taylor rule to conduct monetary policy, then the lower bound on interest rates no longer binds, and the time has come for the FOMC to lessen its accommodative stance by raising the federal funds rate.

Alternative Natural Rate Measures

Another view is that the natural rate can change over time in response to fundamentals. Based in the theory of economic growth, the real interest rate increases as the growth rates of productivity and the population increase. One simple approach to estimating the natural rate is to use population and productivity data. In contrast to the traditional 2 percent natural rate, this approach implies that the natural rate varies over time because population growth and productivity growth change over time. Moreover, one can calculate this time-varying natural rate, under the above assumptions, because one can measure population and productivity growth.⁵

The purple line in the figure above plots the Taylor rule implied interest rate based on the time-varying natural rate. Over the past 10 years, except for one year beginning in mid-2009, the rates implied by this modified Taylor rule and the standard Taylor rule track each other very closely. Most significantly, the policy rate implied by the modified Taylor rule is above both the lower bound and the current real effective federal funds rate over the past year, thus also prescribing that the FOMC should begin to raise the federal funds rate.

Another calculation of the natural rate, which also has theoretical underpinnings, emerges from the observation that the real interest rate is tied to the growth rate of per capita consumption in many economic models.⁶ In these models, the natural rate and the actual real interest rate can differ, however, because of frictions such as nominal price rigidities. One way to control for these frictions is to use a smoothed series for consumption growth rather than actual consumption growth in calculating the natural rate. The red line represents the Taylor rule policy rate using a consumption-growth-based natural rate, estimated with a five-year average of the annualized consumption growth rate.

Notice that this version of the Taylor rule puts the policy rate well above the current real effective funds rate as well as the real rate lower bound. Thus, the consumption-growth natural-rate-based rule also prescribes that the FOMC should begin to raise the federal funds rate.

For a final measure of the natural rate, I looked to John Williams, president of the Federal Reserve Bank of San Francisco, and Thomas Laubach, director of monetary affairs of the Board of Governors: Their alternative method for estimating a time-varying natural rate is constructed, in part, with a statistical technique known as Kalman filtering.⁷ The green line in the figure above represents this rate.

For most of the sample, the Laubach-Williams implied interest rate tracks the other Taylor rule policies very closely. The most significant departure occurs in the past two years. The interest rate implied by the Taylor rule using this natural rate measure shows a much smaller increase than the other three coming out of the most recent economic downturn. Moreover, that rate remains below the lower bound (black line) at the present time, which suggests that this particular formulation of the Taylor rule implies that the time has not yet come for the FOMC to begin raising the federal funds rate.

Current Applications

The above exposition on liftoff and the natural rate isn’t purely academic. Board of Governors Chair Janet Yellen in recent public communications has discussed the Taylor rule in the context of time-varying natural rate models.⁸

Taylor's rule now calls for the federal funds rate to be well above zero if the unemployment rate is currently judged to be close to its normal longer-run level and the "normal" level of the real federal funds rate is currently close to its historical average. But the prescription offered by the Taylor rule changes significantly if one instead assumes, as I do, that appreciable slack still remains in the labor market, and that the economy's equilibrium real federal funds rate--that is, the real rate consistent with the economy achieving maximum employment and price stability over the medium term--is currently quite low by historical standards.

Monetary policy rules provide useful yardsticks against which to compare actual FOMC policy actions. I have examined four Taylor rules which each use a distinct measure of the natural rate. All except one of the four place their corresponding Taylor-rule-prescribed target rates above the current federal funds rate as well as the lower bound. Therefore, all but one suggest that the time for liftoff has come.

Notes and References

¹ Laubach, Thomas; and Williams, John. “Measuring the Natural Rate of Interest,” Review of Economics and Statistics, November 2003, Vol. 85, Issue 4, pp. 1063-1070.

² See Taylor, John B. “A Historical Analysis of Monetary Policy Rules,” Monetary Policy Rules, University of Chicago Press, 1999, pp. 319-348.

³ I constructed real interest rates by subtracting inflation from the corresponding nominal rates. I measured inflation using the year-over-year percent change in the consumer price index (less food and energy).

⁴ The concept of a real rate lower bound is no doubt a loose one, since this lower bound can be breached. In an environment with stable actual and expected inflation, however, one should not see prolonged periods where the real rate is below the lower bound.

⁵ The population is measured as the civilian noninstitutional population (16+ yrs). Productivity is measured as business sector total factor productivity. Both growth rates are calculated as the 12-quarter average of annualized rates of growth for each quarter. I thank Kevin Kliesen for providing me with the population-productivity-based natural rate measures and the underlying data.

⁶ According to this approach, the natural rate also depends on households’ “rate of time preference,” which is time invariant in most economic models. I assumed this term equaled zero in the calculations above. Adding a constant rate of time preference simply shifts natural rate values up, making it less likely that the natural rate lies beneath the lower bound.

⁷ Laubach, Thomas; and Williams, John. “Measuring the Natural Rate of Interest,” Review of Economics and Statistics, November 2003, Vol. 85, Issue 4, pp. 1063-1070. Their baseline estimates, updated through the end of 2014, are also available. See also Williams, John. “The Decline in the Natural Rate of Interest,” Federal Reserve Bank of San Francisco, March 2, 2015.

⁸ See Yellen, Janet. “Normalizing Monetary Policy: Prospects and Perspectives,” Speech at the Federal Reserve Bank of San Francisco, March 27, 2015.

Additional Resources

• Economic Synopses: Liftoff and the Natural Rate of Interest
• On the Economy: What Drives Long-Run Economic Growth?
• On the Economy: How Accurate Are Measures of Inflation Expectations?